(Recursive Universal Selective Artificial General Intelligence)
図解イラストによるRUSAGIの説明です。難しい数式はなく、専門的な知識も必要ありません。知能とは何か?というところから説明します
目次
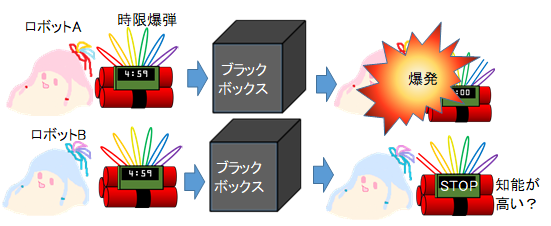
一般的に、人工知能の優劣は、目的の仕事をさせて、結果の優劣で評価します。例として、時限爆弾を止める場合を考えてみましょう。ブラックボックスだとしても、爆発を止められなかったロボットAよりも、止められたロボットBの方が優秀と感じます。
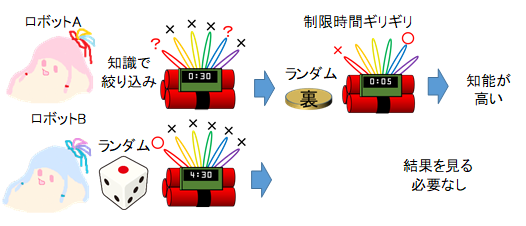
しかし、ロボットBはランダムに行動しているだけと知れば、運が良かっただけで優れているとは感じないでしょう。そこで、運の要素を排除した知能の優劣を定義してみましょう。時限爆弾には切れるコードが6本あり1本が正解とします。ロボットAは、過去のデータを元に2本にまで候補を絞り込んで、時間制銀ギリギリで、2本から1本をランダムに選んだとしましょう。結果とは無関係に、ランダムではない方法で、より少ない本数まで絞り込めた方が優秀だといえます。ただし、ランダムでなければ何でも良いわけではなく、爆発を止めるという目的が設定されているなら、その目的に合致する規則で絞り込まなければなりません。そこで、知能を次のように定義します。
知能の定義: 目的の規則にそって、選択肢を絞り込む能力
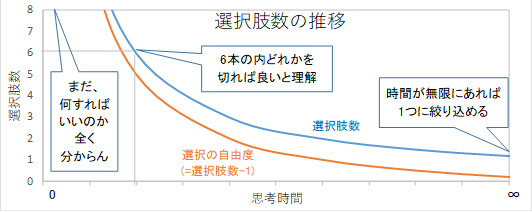
次に、知能の優劣を数値化してみましょう。選択肢を絞り込むのが速いほど、優れているといえるでしょう。計算能力は有限ですが、問題を解くのに必要な情報は与えられているとしましょう。時間が無限に経過した後は、正解の選択肢1つに絞り込めます。逆に時間がゼロのときには、6本の内どれかをカットすれば良いことさえ分からず、それ以外の行動をする選択肢も存在し、選択肢の数は無限にあります。残存する選択肢数は、無限大から始まって時間経過で1に収束します。選択肢数から1を引いた値を選択の自由度とすれば、時間が無限のとき、自由度は0となります。選択肢が減る速度は、時間と共に変化しますが、次式の値は定数に近くなります。
知能定数[個・s] = 選択の自由度[個] × 時間[s]
プランク定数[J・s] = エネルギー[J] × 時間[s] 似ている?
この式で表される定数は、不確定性原理を示すプランク定数と似ています。仮に、素粒子がいくつのエネルギーを取るべきかを選択肢とすれば、選択肢数×時間となり、単位が一致します。素粒子の位置を観測する場合を、爆弾処理の場合と対比してみましょう。
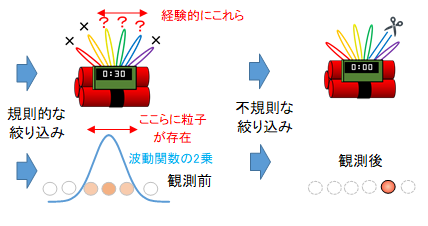
素粒子nの存在位置は完全なランダムではなく、波動関数によって規則的にある程度絞りこまれています。観測することによって、そこからさらにランダムに絞り込まれます。時限爆弾のときと同じような過程といえます。

これに限らず、あらゆる遷移過程は、次にどうあるべきかという選択をしているといえ、その選択肢の絞り込む過程は、規則的な成分と不規則な成分に分けられます。完全なランダムでなければ良く、脳にも素粒子にも知能があるといえます。脳と素粒子の違いは、目的設定と、ハードウェアの能力の差があるだけです。素粒子は記憶力がないため、現在の状態のみから、次の瞬間の状態を選んでいるのに対して、脳は過去の記憶から、先の未来でどうするかも選ぶことができるだけで、根本的なアルゴリズムは同じです。
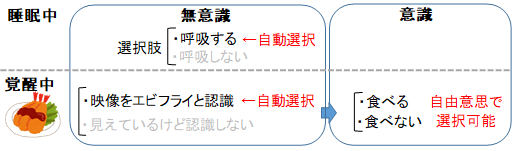
一般的に、意識がある状態とは、覚醒し、感覚器官からの情報を認識できている状態を指します。意識がどういった働きをしているのか考えてみましょう。睡眠中に呼吸するのは意識の働きではありませんが、目の前にエビフライがあるのを認識して、食べようと動くのは意識の働きといえます。動かないという選択肢もあったけど、自由意思によって意識的に動くという選択をしたと言えます。一方、睡眠中の呼吸は自由に選択できません。過程を分解すると、視覚情報からこれはエビフライだと認識する過程と、食べるべきだと判断して運動神経へ出力する過程に分けられます。エビフライが視野に入れば自動的にエビフライが見えていると認識するので、認識するかどうか自由に選択できないため、この過程では意識は働いていないといえます。

では、自由に選択できるとはどういうことか、ディープラーニングと強化学習を組み合わせたものを考えてみましょう。映像から現在置かれている状況が過去のどの状態に近いか選ぶ過程と、その状態でより報酬がもらえる行動を選択する過程に分けられます。ニューラルネットワークの浅層から深層へ情報が流れるのとともに選択肢が絞られると考えられます。無限ループしないように一方向にしか流れないため、一定時間で、最深層まで計算されます。最深層でも最適解といえるまで選択肢が絞り込まれていないかもしれませんが、それ以上、計算することがないので、その時点での最適解を即時出力します。エビフライが見えたら即時、食べるor食べないでどちらが報酬の期待値が大きいか判断して、行動を開始します。
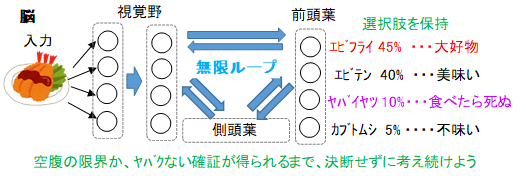
一方、脳の場合は、領域間にさまざまな繋がりがあり、ループしている部分があります。エビフライを認識した瞬間、直感的に、食べるという選択肢が優勢になりますが、必ずしも即座に食べる行動に移るわけではありません。見た瞬間以降も脳内には情報が流れ続けており、すぐに食べる以外の選択肢も考え続けられます。食べる or 食べない or 考えるという選択肢があり、これ以上考えて時間を浪費するより食べるか食べないか決めた方が良いと思うまで考え続けます。決定を下したときには、自由意思で決めたと感じるでしょう。このとき、考える以外の選択肢のどちらが有利とも絞り込めていなければ、ランダムに選ぶことになります。自由意思で選ぶということは、実際にはランダムです。ただ、思考を打ち切るタイミングが外部環境ではなく、脳内の状況で決まるため、自発的に決めたと感じられます。意識の無い深層学習と、意識の有る脳を比べてみましょう。深層学習は層の数等によって一定の範囲内でのみ考えればよいというフレームが決められているため、一定時間で規則的な選択肢の絞り込みが完了し、即座に残った選択肢からランダムに選択します。一方、脳は、短時間で直感的に選択肢をある程度絞り込んだ後、即座にランダム選択へは移行しません。選択肢を保持したまま、考慮するフレームを拡大する等して、選択肢のさらなる規則的な絞り込みを継続します。経験的に関係の強いことから考慮をはじめて、決断を迫られるまでフレームを拡大し続け、時間が無限にあるなら、関係なさそうな全てことも考慮して最適解へ近づき続けます。
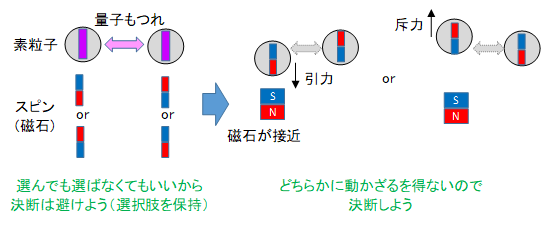
このような、必要に迫られるまで選択肢を保持するという現象は素粒子にもみられます。対生成した粒子のスピンは保存則を満たすために合計で0でありさえすればよく、上向きと下向きが重なった状態になります。他の粒子を近づけると、引力or斥力が働かなければいけないため、どちらかに決まります。観測前から上向きor下向きのどちらかに決めてあったとしても保存則を満たしますが、そうはなりません。次のような原理があると解釈できます。
選択肢保持の原理: 必要に迫られるまで選択肢を保持する。
(複数の状態を取ることが許されるなら、どれか一つの状態を取らない)
意識とは、より良い選択をするために、必要に迫られるまで選択肢を保持する仕組みで、次のように定義します。
意識:より良い選択をするため、必要に迫られるまで選択肢を保持する仕組み
物質でしかない脳になぜ意識が宿るのかというと、素粒子にも意識があり、脳が感じている意識というものは、素粒子が感じている場に相当すると解釈できます。

知能を持ったシステムの構成要素として、①ハードウェア、②ソフトウェア、③データの3つに分けられます。ハードウェアの変更なしで改変できるのが②③で、ソフトウェアの変更なしで改変できるのが③となります。
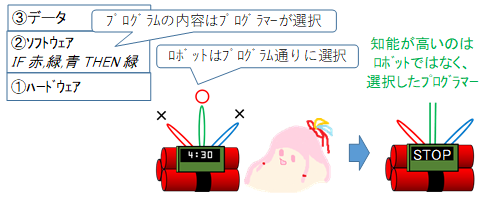
時限爆弾処理ロボットの例を考えてみましょう。プログラマーが事前調査を元にして、「IF(コードが赤,緑,青の3本)THEN 緑を切る」とプログラムしたとします。これは、②ソフトウェアに当たります。このプログラムを搭載したロボットが良い結果を出したとします。このとき、一見ロボットが優秀に見えますが、ロボットは決められた通り動いているに過ぎません。知能とは選択する能力なので、知能が優秀なのはロボットではなく、どう動くか選択したプログラマーといえます。
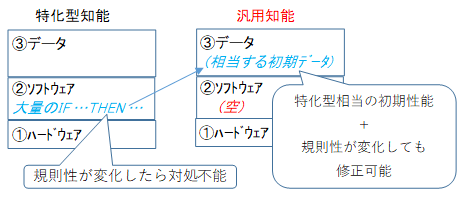
また、未来で正解の規則が変化したときに、IF文が固定されていると対応できません。汎用性を高めるには、②ソフトウェアとして固定されたパラメータはできるだけ減らす必要があります。例えば深層学習での層数は、状況によって最適値が変わるので固定すべきではありません。あらゆるパラメータが動的で、常に最適値を選択できるのが理想的です。脳でさえ理想とはいえません。
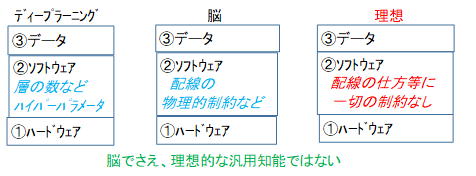
ニューラルネットワークを5次元的に配線した方が良いけど、物理的制約で出来ないだけかもしれません。人工知能は脳の物理的制約を真似て、性能を制約する必要はありません。知能の定義さえ正しく決められれば、脳を真似る必要が無く、一切の固定パラメータや制約のない究極の人工知能が可能になります。究極のアルゴリズムは、こうあるべきだとプログラマーが固定した定数値や処理がなく、シンプルなものになるでしょう。シンプルで空っぽなプログラムより、IF・THEN文のような知識を大量に詰め込んだプログラムの方が優れているという見方もできますが、IF・THEN文に相当する情報を③データとして持たせればよく、特化型人工知能が汎用人工知能より優れることはありません。
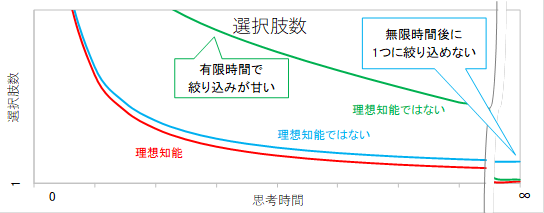
ただ固定パラメータがないだけでは、理想的な知能とはいえません。仮に、問題を解くのに必要な情報が与えられているなら、十分に時間が経過した後は、正解の選択肢1つに絞り込めてなければいけません。情報が不十分でも、その範囲でできるだけ絞り込まなければいけません。また、十分に時間が経過する前でも、できるだけ絞り込まなければいけません。理想的な知能を次のように定義します。
理想知能: 常に、目的に合致するように、あらゆる選択肢をできるだけ絞り込む
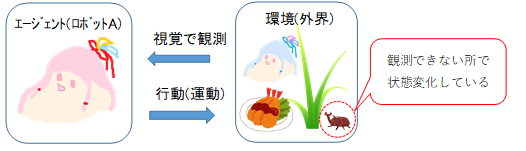
一般的な強化学習のモデルでは、エージェント(ロボットA)と環境が情報をやりとりします。エージェントは感覚器官によって環境の状態を観測します。ある状態に対して報酬が定められていて、報酬の期待値が最大になる行動を選択し、運動器官によって環境へ影響を与えます。それにより環境が変化しますが、観測できるのは環境の一部分だけで、見えない部分でも変化が起こっています。
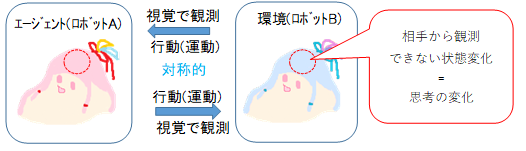
逆に環境の方から見れば、エージェントの運動を受け取って、感覚器官へ返答しています。環境は外部の世界全体ですが、別のロボットBだけに限定しても成り立ちます。お互い対称的に、相手の運動を観測して、自分の運動を選択するという形になります。ただし、環境のときと同様に、相手から観測できないところで変化している状態もあり、どう行動するかを選択するだけでなく、その見えない状態をどうするかも選択しています。運動ではない、見えない状態変化というのは、何を考えているかの変化に対応するといえます。

一般的な強化学習モデルが、どう出力するべきかだけを選択するのに対して、脳は運動神経への出力だけでなく、脳内部の他領域への出力をどうするのかも選択しているといえます。つまりは、どう動くか考えるだけなく、何を考えるべきかについても考えています。
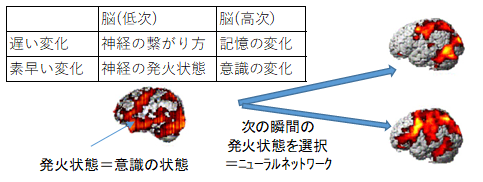
ここでの考えるとは意識の状態の変化でもあります。意識の状態は素早く変化することができますが、脳の持つ情報には、素早く変化するものと、遅いものがあります。遅い方はニューラルネットワークがどのように繋がっているかという情報で、速い方は、現在どのニューロンが発火しているかの情報です。意識の変化は、発火状態の変化と推測できます。では、ネットワークの役割はというと、現在どのニューロンが発火しているのかという入力に対して、次の瞬間にどのニューロンを発火させるのかを選択して出力しているのに過ぎません。脳を客観的にみれば、ただ選択するという知能の原理となる処理をしているのに過ぎないと解釈できます。
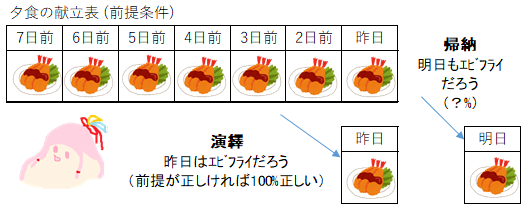
一般的な強化学習では、次の瞬間から未来永劫までに受け取る報酬の合計の期待値を最大にするのが目的です。その期待値は演繹ではなく、帰納的に推論します。例えば過去1週間の夕食がエビフライだというのを前提として、昨日の夕食はエビフライだろうという結果が演繹、明日もエビフライだろうという結果が帰納です。演繹では、結果の情報が前提に含まれているため、前提が正しければ結果も正しい。一方、帰納は、知らないはずの未来の情報が追加されており、正しいとは限りません。確証性の原理によれば、関連する観測が増えるほど結果の確からしさが増すとされていますが、具体的にどういう観測がどれだけあれば○○%正しいといったようには示されておりません。
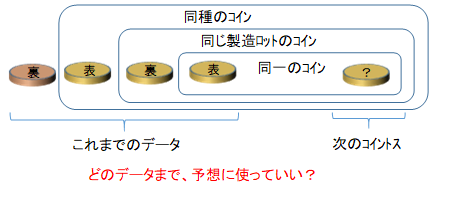
例えば、コイン投げの場合、データが多ければ問題ないように思えますが、データとして、同一ではないが同じ製造ロットのコインを投げた結果も含めてよいのかといった判断基準はありません。機械は人間が選定して打ちこんだデータが有効という前提で計算するのみです。そこで、確証性の原理を次のように再定義します。
確証性の原理 : 証拠の質と量が増すほど、帰納の確証性が増す
確証率という値を次式で定義します。0であれば全く分からず、1であれば必ず真となります。
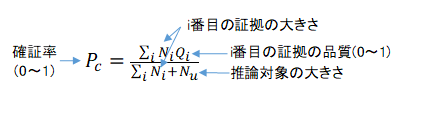
まず証拠の品質=1、推論対象の大きさ=1の場合を考えてみましょう。

確証率は、証拠の数と推測しようとしている数の比で表されます。例えばコイン投げで、次回表が出るという推測と、次回と次々回ともに表がでるという推測では、後者の方が確証率は低くなります。確証率とは、推測しようとしているものも含めて、知っていることと知らないことの数の比をとっています。
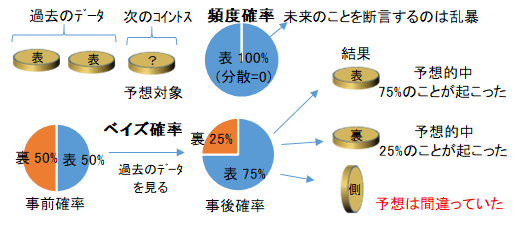
コイン投げの具体例で表裏の確率を求めてみましょう。表が2回連続で出たという前提で、次の表裏を推測しましょう。まず一般的(頻度論的)な確率の計算方法ですと、表を1、裏を0として、平均値は1、分散は0と推測できます。分散が0なので、100%表という推測ですが、未来に起こることはどんなことでも100%とはいえません。常識的な物理法則でさえ、現在までに反例がないだけで、今後も成り立つ証明にはなりません。ベイズ確率では、50%表,50%裏という事前確率を前提条件とすれば、75%表,25%裏という事後確率が推測できます。しかし、コインの側面が下になるということが起こった場合、推測は外れたことになります。これら2つの手法は、前提にない情報が結果に含まれてしまう帰納的推論ですので、必ずしも予想は的中しません。
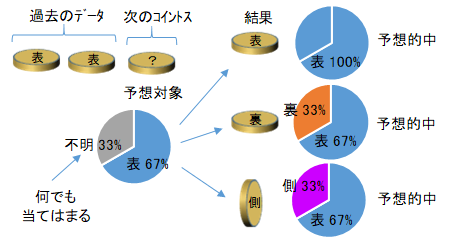
そこで、確証率の考え方で推測してみましょう。確証率の分母は、証拠(既知の標本)と推測対象(未知の標本)から成るため、それらの構成比をそのままグラフにしてみましょう。既知の表の標本が2つなので67%は表、未知の標本は1つなので33%は"不明"と推測されます。ここでいう"不明"は、どんなものにでも当てはまるとします。すると、結果が表や裏の場合だけでなく、側面が下を向くような奇跡が起こったとしても、予想が的中したといえます。不明と推測では、知りえない未来の情報を知っているかのような主張はせず、情報量は増えないため、演繹的推論といえます。
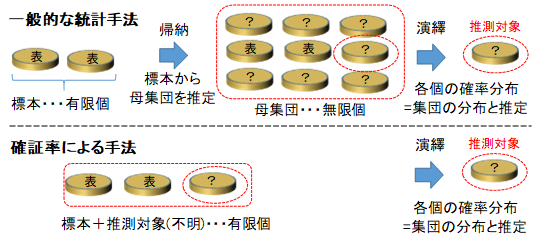
一般的な統計では、標本から母集団を推定することで次の標本を推測しますが、ここでの方法では、予想対象を"不明"という値を持つ標本として追加して、標本集団の分布を求め、大数の法則により、標本の確率は、標本集団の分布に等しいと推測します。一般的な統計では、本来"不明"であることにも尤もらしい値を割り当ててしまうため、標本数が少なると信頼性が低下してしまうため、ビッグデータが不可欠になってしまいます。一方、"不明"を"不明"まま扱い続けた場合なら、データが少なかったり、推測に推測を重ねたりしても、真理は保たれて続けます。次に、証拠の品質が1ではなく、0.5の場合を考えてみましょう。証拠の品質というのは、予想しようとしている値(コインの表裏)の確率分布が、予想対象のものの確率分布と同じである度合を表します。例えば確率分布Aのコインを次に投げた結果を予想します。標本(証拠)とするコインは50%の確率分布Aを持っているとします。無限回、標本コインを投げてすべて表の場合、品質=0.5として確証率を求めると次になります。
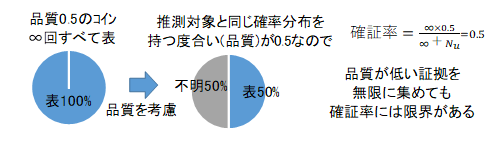
無限回やれば標本コインの持つ確率分布は100%分かりますが、そもそも標本コインが予想対象と同じ確率分布を持つ確率が50%なので、いくらやっても50%以上の確証は得られません。次に、さまざまな証拠の品質の値を持つものが混在している場合を考えましょう。
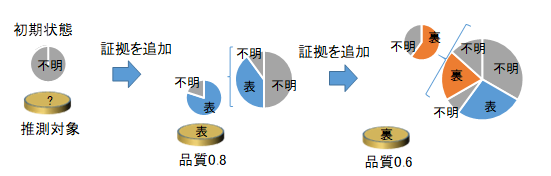
品質を考慮して分布を推測する場合、まずは"不明"が1個あり、品質0.8で表という証拠があれば、"表"の証拠が0.8個、"不明"の証拠が0.2個を追加という操作を、採用したい証拠について逐次行うことで求められます。
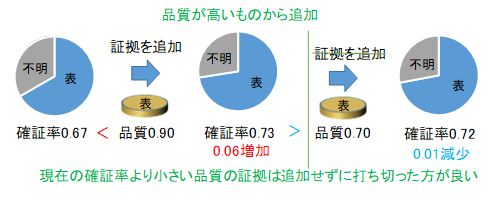
品質が既知であれば、品質が高い証拠から採用していくことで、効率よく確証率を上げられます。品質が現時点での確証率より大きい場合は、採用することで確証率が増加しますが、逆に確証率より品質が低いものを採用すると確証率は減少してしまいます。相対的に品質が低いものについては、証拠は多ければ多いほどよいわけではありません。これ以上、採用しても逆効果の証拠しか残っていない時点で、計算を打ち切ればよいので、ひょっとしたら関係があるかもしれない程度の低品質の証拠が大量にあっても、効率よく無視することができます。

また、品質の良い証拠が無ければ、品質の悪い証拠を使えばよいので、証拠がなくて推測ができないという状況はありません。例えば、あるリンゴの味を推測したいとします。同じ品種の味を知っていればそれで推測しますが、さもなければ別の品種のリンゴの味から推測します。もしエビフライした食べたことがないなら、リンゴもエビフライも食べ物という同じカテゴリのため、同じ味がするだろうと推測できます。見方によっては、同個体のリンゴであっても齧る場所によって、素粒子は別個体なため別の味だと推測できますが、別の見方をすれば、この世のすべての物体は、同種の素粒子からできているので、同じ味だと推測できます。
演繹的推論では複雑なことでも三段論法のような基本形に分解できますが、帰納的推論はどう分解できるでしょうか。例えばある値が20±10くらいだろうという主張は、10以上だろう、30以下だろうという二つの主張に分解できます。上限か下限しか推測できない場合でも、何も推測できないよりは有用です。限界まで分解して、その一つでも主張できるようにしましょう。これ以上分解できない帰納の要素は次のように考えられます。

帰納の原理:独立変数が近いほど、従属変数が近いと推測する
関数の独立変数(引数)が近いほど、従属変数(戻り値)が近いと推測します。例えば、時刻t0のときの温度がTいうことと、時刻t1は時刻t2よりもt0に近いことだけが既知だとします。時刻が完全に一致すれば、温度も完全に一致します。このとき、時刻t1の温度T1が、T2よりもT0に近いということだけが推測できます。数値としていくつか、またどのくらいの確証があるかも数値化できません。情報として、不等号しか与えられていないため、不等号でしか推測できません。こういった不等号を積み重ねていけば順序や数値が推測できるようになります。

引数が複数あっても同じことがいえます。引数が、時間tと位置xの場合を考えます。時間差と距離のどちらかが0か、大小関係がどちらも同じなら、先ほどと同じように推測できます。しかし、時間差が大きく距離が小さいものと、時間差が小さく距離が大きいものでは、単位が違うため、どちらの方の温度が近いか推測できません。しかしながら、平均値についても同じ式が適用できます。

位置1のさまざまな時刻に測定した平均温度と、位置2のさまざまな時刻に測定した平均温度では、位置1の方が位置0に近いなら、平均温度も位置1の方が近いと推測できます。このとき、位置以外については無作為にデータを選んでいるため、標本数が増えれば、平均値は同等だろうとみなしています。

ここでは、位置と時間だけで温度が決まるとの前提条件がありますが、現実では前提条件がなく、何が関係するのかわからないため、あらゆる特徴量を、関数の引数にしなければなりません。特徴量が無数にあるため、重回帰分析などで何が関係するか調べるのも困難です。しかし、先ほどの平均値を推測する方法なら、ある引数(特徴量)にだけ着目して、残りの無数にある特徴量は無視することができます。不等号での大小関係のみの推論は、ワンショットラーニングと呼ばれるような一度だけの経験での学習にとって重要です。
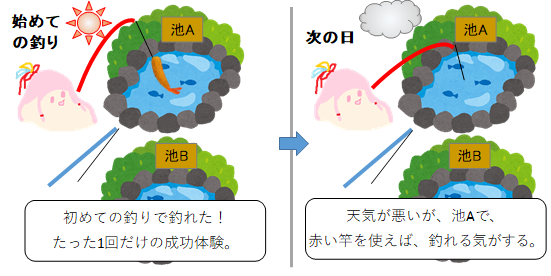
例えば、ある晴れた日に、初めての釣りで、赤い釣竿を持って池Aへ行き、エビを釣り上げたとします。青い釣竿も持っており、池Bという釣り場もあるとします。エビが欲しいため、翌日、曇っていたけど、赤い釣竿で池Aへ釣りに行きました。

なぜそう判断したのか考えてみましょう。エビが釣れるならTrueを返す関数を考えます。引数は"釣場"と"その他条件"の2つとします。"釣場"="池A"ならTrueと仮説を立てます。1度の成功経験が既知の証拠1個になり、翌日釣れるかどうかは未知のため、未知の証拠(不明)が1個になります。したがって、釣れる確証率は50%となります。"その他条件"以外の条件が満たされていたら証拠の品質は1で、確証率は、"その他条件"が満たされる確率とも解釈できます。別の仮説も立てましょう。引数が"釣場","天候","竿の色","その他条件"とします。後者の仮説では、天候と竿の色も合っていれば、確証率50%、さもなければ0%です。同じ50%でも、前者と後者の仮説では、"その他条件"の範囲が異なるため、確証率の大小を直接比較できません。しかし、後者の"その他条件"が真の場合は、前者の"その他条件"も真になるので、証拠の個数は同じでも、後者の方が高品質いといえます。どんな条件についても、できるだけ成功例に近づければ、"その他条件"の範囲を狭めることができます。赤い竿が青い竿よりどれほど優れているのかは分からないけど、どちらかといえば赤い方が良いとだけいえます。天候のように操作できないものもありますが、近づけられるものは近づけた方が良いと判断します。どちらが良いかという不等号が推測できるだけで、こうすれば○○%釣れるというように推測できるわけではありません。

選択肢を絞り込むアルゴリズムを考えましょう。名前付き写真データが大量にあり、推測対象映像(エビフライ?)の名前を推測する場合を考えます。いつ決断が迫られるか分からず、決断を迫られた時点で、回答しなければなりません。もし、思考時間が全く与えられなかった場合、全ての写真データについて同様に確からしいため、全写真の名前の分布がそのまま推測値になります。

各写真は品質値(0~1)を持ち、それは名前の確率分布が推測対象と一致する確率の上限を表します。初期状態では全写真が品質値=1であり、名前の分布が一致する確率が1以下と示しています。各写真の品質値を徐々に更新することで、徐々に選択肢を絞り込んでいきます。決断時、例えば品質値0.1の写真は0.1個として重みを付けた、全写真の名前の分布が、推測値となります。映像の特徴が似ているほど、品質値が高いと推測できます。
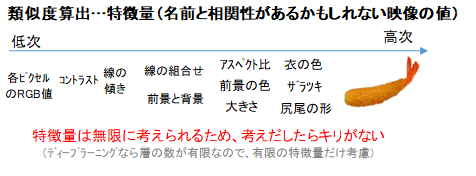
しかし、特徴といっても、尻尾の色・向き・大きさ、衣の色・ザラツキ・アスペクト比など、さまざまな特徴量があります。単純な特徴量を組み合わせて新たに複雑な特徴量を作ることもできます。そのため特徴量は無限にありますが、どの特徴量が近いと名前が近いのかを計算しなければいけません。正確に計算しようと無限にある特徴量を調べようとすれば、無限に時間が掛かってしまします。ディープラーニングの場合では、深いほど複雑な特徴量を捉えられますが、深さは有限のため、一定以上に複雑なことは考えずに計算を打ち切ります。理想的には、無限に時間があれば、無限に複雑なことまで考慮し、無限に精度を上げ続けられる必要があります。有限な時間では、有限の特徴量しか考慮できないので、どの特徴量を考慮するか選択しなければなりません。過去の経験等から、どの特徴量が有効そうかの知見があれば、有効そうな特徴量から考慮することで、効率よく絞り込みが行えます。
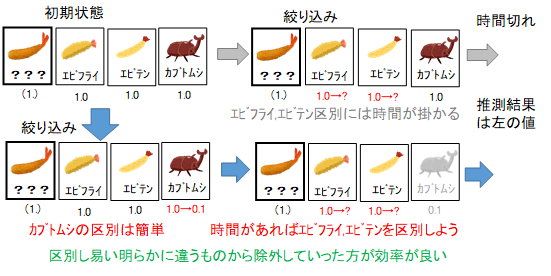
効率よく絞り込む戦略を考えていきましょう。エビフライとエビテンは似ており、ある特徴量で線引きするのは難しいでしょう。どう見てもエビテンなのにエビフライと名前のついた写真があれば、どんなに複雑な特徴量によっても完全に分離できない可能性もあります。一方、エビフライとカブトムシは、比較的簡単に見分けられるでしょう。先に明らかに違うだろうというカブトムシを除外して、後で時間に余裕があればエビフライかエビテンか熟考すれば良いでしょう。
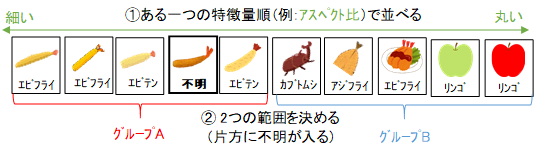
具体的な計算方法を考えてみましょう。まず、全ての写真は、説明変数(特徴量)、目的変数(名前)、品質値を持っています。推測対象の名前は"不明"となります。特徴量は、各ピクセルの色のような低水準の値から、尻尾の大きさのような高水準の値も持っています。まず、ある一つの特徴量を選択します。その特徴量の値で、全写真を分類します。(その値の順で写真を並び替えます)。次に、その特徴量の値の範囲を2つ決めます。2つの範囲は重複せず、片方には推測対象が含まれていなければいけません。
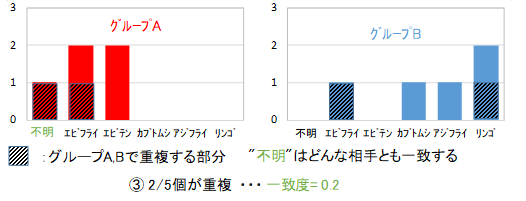
次に、2つの範囲それぞれに含まれる全ての写真の名前について、ヒストグラムを作製します。2つのヒストグラムが一致する度合いを"一致度"(0~1)としましょう。一致度は、簡単にヒストグラムが重なる部分の面積として計算できますが、2集団が同じ母集団から抽出されたという帰無仮説がどの程度棄却できるかと計算しても良いでしょう。ただし、"不明"については、どの値とも一致するとして、最大でどれだけ一致するか求めなければなりません。2集団のうち、推測対象が含まれる方を集団A、他方を集団Bとします。2集団の一致度が0.2であったとしましょう。
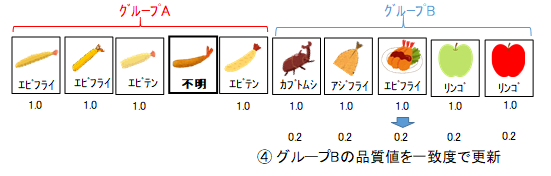
この一致度で、集団Bに含まれる全ての写真の品質値を更新します。品質値=一致度となりますが、現在の品質値が一致度より低い場合は、更新せずに低い方を保持します。一致度が低い場合は、説明変数(特徴量)と目的変数(名前)に相関性が高いことになるので、推測対象と特徴量が異なる集団を除外することで、推測対象と似たものが残ります。逆に、一致度がほぼ1の場合は、相関性がないため、片方の集団を除外することは無作為抽出となります。標本の数を無駄にすり減らすべきではないので、一致度が高ければ、除外せず保持します。
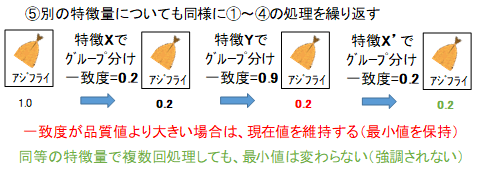
ここまでが1サイクルで、次は別の特徴量と2範囲を選択して、同様の処理を繰り返します。品質値は小さくなる場合だけ更新するため、相関性のない特徴量を選んでしまっても、前ステップまでの結果は消えません。また、全く同じ処理を2回行ってしまっても、品質値は更新されないため、その特徴量が重視されてしまうことはありません。2範囲を決めるとき、範囲を広く取りすぎると多種多様な写真が混在するため、一致度は上がってしまします。逆に範囲を狭くし過ぎると"不明"の比率が増え一致率があがります。また、1ステップで除外できる写真が減るため、少なすぎても良くありません。

これらの処理は、彫刻と似ています。まず木の塊から不要な部分を大胆に除去し、徐々に細かく彫り込んでいきます。これ以上細かく彫っても、商品価値の増加より、加工費の増加の方が大きいと判断したところで終了し出荷します。もし不意に出荷指示が出されても、荒く彫ったそれなりのものが出荷できるでしょう。一方、ディープラーニングのようなものは3Dプリンターに近いでしょう。一定の精度で、下から順に作っていき、一定時間で完了します。途中で出荷指示が出ても、下半分しかできてなければ商品になりません。また、完了後にもっと時間を上げるから精度を上げてくれと言われても対応できません。
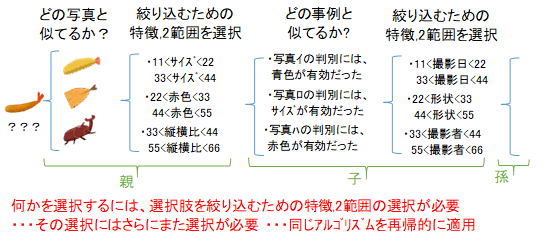
選択肢を絞り込むアルゴリズムの各ステップでは、特徴量と2範囲を選択しなければいけません。過去に、どの特徴量でうまくいったかというのを調べることで、適した特徴量を選択します。では、その選択はどうやって行えばよいかというと、同じアルゴリズムを適用します。
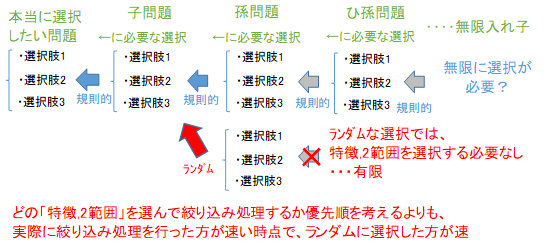
選択するために必要な選択を、再帰的に行うため、選択しなければいけないことが無限にあります。しかし、フリーズしてしまうことはありません。計算する時間がなければ、すべて同等に確からしい(品質値=1)と判断して、そこからランダムに選択してしまいます。ランダムな選択なら、特徴量を選択する必要がなく、それ以上の再帰処理はありません。ある特徴量で、どのくらいの一致度になりそうなのかというのを過去の経験から正確に計算するよりも、ランダムに特徴量を選んで、実際に一致度を算出した方が速いというような状況になれば、ランダムに特徴量を選択することを選択します。
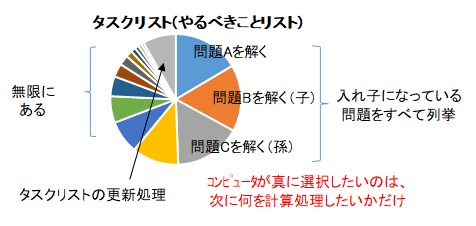
ある選択肢を絞り込むとき、さらに絞り込む処理をするか、それとも残りからランダムに選んでしまうかという、どう処理するのかという選択もあります。選択肢を絞り込むという処理を"タスク"と呼ぶとしましょう。タスクが入れ子になっており、無限にあるようで手が付けられないように感じます。しかし、コンピュータが実質的に行うタスクは、たった1つのみです。それは、次に何を計算(処理)するかを選択しているだけです。そこでタスクリスト(やるべきことリスト)を作成しましょう。入れ子になっている子タスクを全て外に出して、並列に並べてしまいましょう。すべてのタスクが品質値(0~1)を持っており、品質値が高い物から、同じなら無作為抽出で、タスクをこなしていきましょう。
各タスクの品質値を更新するというタスクもタスクリストへ入れましょう。
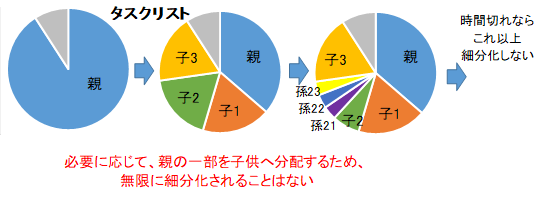
親タスクには、子タスク、孫タスクが入れ子になっていますが。最初は親タスクのみがタスクリストへ入っています。また、その親タスクについて、子タスクをタスクリストに追加するというタスクがあります。そのタスクが実行されて初めてリストに随時追加されるため、タスクリストが無限個のタスクで一杯になることはありません。
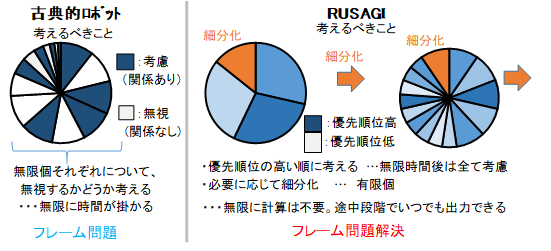
このアルゴリズムでは、フレーム問題が発生しないのが分かります。一般的なフレーム問題では、最適解を求めるには無限にあることを計算しなければならないため、関係あることだけ考えようとします。しかし、無限にあることの各個について、関係あるかどうか考えると、無限に時間が掛かってしまいます。人間はどうしているのかというと、関係あるorなしデジタルな2択ではなく、関係の深そうなことから考えて、時間に余裕があれば、徐々に関係の浅いことも考えていると思います。何について考えるのかというのは先ほどのタスクリストに相当します。そのタスクリストでは、考えるかどうかの順位づけに時間を割くよりも、実際に考えた方が速いと判断すれば、順位付けはある程度ランダムに行え、また、リストの追加も必要に応じて随時維持行うため有限なので、無限に計算してしまうことはありません。ここまで説明してきたアルゴリズムを再帰的に普遍的な選択をする人工一般知能(汎用人工知能)Recursive Universal Selective Artificial General Intelligenceの頭文字をとってRUSAGIと呼ぶことにします。

このシンプルなアルゴリズムで人間のような高度な思考ができるのか、具体例で考えてみましょう。ロボットには映像が入力され、どの筋肉を動かすかという出力の選択ができます。満腹になるのが報酬で、目的とします。満腹感もまた、ロボット内部のセンサーによる入力とみなせます。生まれたばかりでは、止まっている方が良いという知識もないため、ランダムに運動します。偶然、口にエビフライが入ると、入力と出力の関係を考えて、同じ状況を再度起こそうとします。体をどう動かすかというパターンの中から、良いものを絞り込んでいきます。その選択のための説明変数(特徴量)は、初期状態では、映像の1ピクセル毎の色がどうかという単純なものしかありません。中央付近のピクセルの色が明るいときに、ある筋肉に力を入れれば、そうでないときと比べて、その後、報酬が得られたことが少し多いというような学習をするでしょう。次第に、ピクセル×各筋肉の関係性は浅く、これ以上考えても報酬がほとんど増えないと判断し、複数のピクセルの色を組み合わせたコントラストや線の傾きといった特徴量について考えるのに時間を割き始めます。同様にして、だんだん高度な概念を考えるようになります。